Algorithms¶

Line strafing¶

Line strafing refers to the act of strafing along a fixed line towards a particular direction. It is not possible to strafe so that the path is a straight line, therefore we have to choose the strafing directions (either left or right) carefully to approximate a straight path and minimise the deviation from the path. We will describe the approach used by TasTools mod here.

Recall that every line in $ℝ 𝑛$ can be represented as a parametric equation $𝐫 = 𝐚 + 𝑠 𝐛$ , such that the line is the locus of $𝐫$ , $𝑠$ is the parameter, $𝐚$ is a known point on the line and $𝐛$ is a vector parallel to the line. In the context of line strafing $𝐚$ is called the origin of line strafe (OLS) and $𝐛$ is the direction of line strafe (DLS). For simplicity we often normalise $𝐛$ . Let $𝐩$ be the player position, then the distance of the player from the line is given by

∥ (𝐚 - 𝐩) - [(𝐚 - 𝐩) \cdot ˆ 𝐛] ˆ 𝐛 ∥

To line strafe, we would use Equation (6.4) to compute two different player positions corresponding to left and right strafe. Then the distances of these positions from the line is compared, the direction that causes the smallest deviation from the line is chosen to be the final strafing direction for this particular frame.

The advantage of this method is that it allows some control over the amplitude of line strafe. If the initial player position is relatively far away from the line, then the amplitude of the subsequent path will be approximately equal to the initial point-to-line distance.

In practice, the method to compute $ˆ 𝐛$ depends on the value of $𝐯$ . If $𝐯 = 𝟎$ , then we might set $ˆ 𝐛 = ⟨ c o s 𝜗, s i n 𝜗 ⟩$ , which means line strafing towards the initial viewing direciton. Otherwise, we would set $ˆ 𝐛 = ˆ 𝐯$ . At times we might want to override $ˆ 𝐛$ manually. In TasTools, this can be accomplished by issuing tas_yaw while +linestrafe is active.

Computing strafing inputs¶

Up to this point we have been analysing strafing in terms of $𝜃$ , the angle between velocity and acceleration vectors. To actually strafe in practice, we need to adjust the yaw angle and provide the input (such as +moveright) correctly. In this section we describe a simple algorithm to produce such input.

We start off by computing the intended $𝜃$ in degrees, which is the foundation of all. Now we must set $𝐹$ and $𝑆$ , which can be achieved by issuing the correct commands (+forward, +moveleft, +moveright, +back). Assume that $| 𝑆 | = | 𝐹 |$ and $‖ ⟨ 𝐹, 𝑆 ⟩ ‖ \geq 𝑀$ before PM_CheckParamters is called. In principle it does not matter which of the four commands are issued, but to minimise screen jittering we can adopt the following guideline:

If $0 \leq 𝜃 < 22.5$ then +back with negative cl_backspeed.
If $22.5 \leq 𝜃 < 67.5$ then +back and +move(right|left) with negative cl_backspeed.
If $67.5 \leq 𝜃$ then +move(right|left).

where 22.5 is midway between 0 and 45, and 67.5 is midway between 45 and 90. You must be wondering about the +back and negative cl_backspeed as well. The rationale is this: we want to avoid accidentally pushing movable entities. If you look at the CPushable::Move function in dlls/func_break.cpp, notice that an object can be pushed only if +forward or +use is active.

To compute the new yaw angle, in the most general way we compute $𝛼$ , $𝛽$ and $𝜙$ , all in degrees, where

𝜙 = a r c t a n (∣ 𝑆 𝐹 ∣) 𝛼 = a t a n 2 (𝑣 𝑦, 𝑣 𝑥) 𝛽 = 𝛼 \pm (𝜙 - 𝜃)

Notice the $\pm$ sign in $𝛽$ ? It should be replaced by a $+$ if right strafing and $-$ if left strafing. We must add that if $𝐯 = 𝟎$ then we are better off setting $𝜃 = 0$ and $𝛼 = 𝜗$ . In practice, when the speed is zero what we want is to strafe towards the yaw direction. In this case it does not make sense to have $𝜃$ carrying nonzero values, even though it is mathematically valid. The atan2 function is available in most sensible programming languages. Do not use the plain arc tangent to compute $𝛼$ or you will land yourself in trouble. In addition, we often do not need to compute $𝜙$ in the manner presented above if $| 𝑆 | = | 𝐹 |$ , unless vectorial compensation is employed (will be discussed later).

Now we can compute the following trial new yaw angles, denoted as $˜ 𝜗 1$ and $˜ 𝜗 2$ , such that

˜ 𝜗 1 = a n g l e m o d (𝛽) ˜ 𝜗 2 = a n g l e m o d (𝛽 + s g n (𝛽) 𝑢)

We see a new function anglemod and a new constant $𝑢 = 360 / 65536$ . Anglemod is a function defined in pm_shared/pm_math.c to wrap angles to $[0, 360)$ degrees. Except, it accomplishes this by means of a faster approximation, instead of a more expensive but correct method which may involve fmod. The spirit is not dissimilar to the famous fast inverse square root approximation. The angles produced by anglemod is always a multiple of $𝑢$ . Consequently the strafing may be less accurate, now that the actual $𝜃$ will only be an approximation of the intended $𝜃$ .

The anglemod function truncates the input angle, instead of rounding it. The following optimisation can be done to improve the accuracy slightly. Set $𝜃 1 = ˜ 𝜗 1 \mp 𝜙$ and $𝜃 2 = ˜ 𝜗 2 \mp 𝜙$ which are the actual $𝜃$ s, then use these $𝜃$ s and the scalar FME to compute the new speeds. Now compare the new speeds to determine the $˜ 𝜗$ that gives the higher speed. This will be the final yaw angle.

Autoactions¶

An autoaction refers to a set of input that are generated automatically when certain conditions are met. In TasTools they are (in order of precedence) tas_jb, tas_lgagst, tas_db4l, tas_db4c, tas_dtap, tas_dwj and tas_cjmp. The tables below show the conditions and corresponding actions. If a condition is not displayed, no-op is assumed. Key: og is onground status, d is user +duck input, j is user +jump input, and dst is duckstate. The abbreviation “a.u.” stands for “after unducking”, while “a.d.” stands for “after ducking”.

When we say a command is taken precedence over the other, it means if the former command performs an action all lower precedence commands will be inhibited.

Implementing automatic jumpbug can be tricky. Suppose +duck is not active, player is not onground and falling. We want to make sure the player is not onground after the final groundcheck, which requires predicting the new position after PM_AddCorrectGravity and movement physics. The following is the action table for jumpbug implementation. Jumpbug is usually prioritised over other autoactions. If $𝑣 𝑧 > 180$ then jumpbug is impossible.

If dst 2 AND unduckable AND jumpable AND onground with dst 0, stop with -duck and +jump.
If new position is unduckable AND new position is onground with dst 0, stop with +duck and -jump.

Automatic ducktap is taken priority over automatic jump unless stated otherwise. Recall that ducktapping only works if there exists sufficient space to accomodate the player bounding box if he is moved vertically up by 18 units, while the duckstate is not 2. If the duckstate is 2 then the player must first unduck for this frame. Ducktap is relatively complex:

og	d	j	dst	action
0	0	1	2	`-jump` if unduckable AND onground a.u..
1	–	–	0	`-jump` and `+duck` if sufficient space, automatic jump otherwise.
1	–	–	1	`-duck` and decrement if sufficient space., automatic jump otherwise.
1	–	–	2	`-jump` and `-duck` if unduckable AND sufficient space a.u., automatic jump otherwise.

For automatic jumping, the need to handle pmove->oldbuttons complicates matters. At the time of writing, TasTools assumes IN_JUMP is unset in pmove->oldbuttons. A rare use case for this would be to temporarily disable automatic jumping simply by issuing +jump.

og	d	j	dst	action
0	0	1	0	`-jump` if new position is onground with dst 0.
0	1	1	2	`-jump` if new position is onground with dst 2.
0	0	–	2	Decrement and `+jump` if unduckable AND onground a.u. AND jumpable. `-jump` if new position is unduckable AND new position is onground with dst 0.
0	1	1	0	`-jump` if new position a.d. is onground.
1	0	–	1	Decrement and `+jump` if jumpable AND insufficient space, `-jump` otherwise.
1	1	–	1	Decrement and `+jump` if jumpable, `-jump` otherwise.
1	–	–	0/2	Decrement and `+jump` if jumpable, `-jump` otherwise.

Next we have DB4L. As with jumpbug, if $𝑣 𝑧 > 180$ then this is impossible.

og	dst	action
1	2	Decrement and set state to 0 if state is 1
0	0	`+duck` and set state to 1 if new position is obstructed by ground.
0	2	`+duck` and set state to 1 if unduckable AND (onground a.u. OR new position a.u. is obstructed by onground). Otherwise, decrement and set state to 0 if state is 1.

Then we have DB4C.

og	d	dst	action
0	0	0	Decrement and `+duck` if new position is obstructed OR (new position a.d. is obstructed AND new speed is less than new speed a.d.).

We also have DWJ, which is inserting +duck at the instant the player jumps. This can be useful for longjump and as a jumping style itself. To selfgauss with headshot immediately after jumping usually requires this jumping style to work. There is no action table for this – the counter is decremented and +duck is inserted whenever the player successfully jumps.

Vectorial compensation¶

Vectorial compensation (VC) is a novel technique developed to push the strafing accuracy closer to perfection by further compensating the effects of anglemod. It is called vectorial as it manipulates the values for cl_forwardspeed and cl_sidespeed, thereby changing the direction of $ˆ 𝐚$ slightly. This technique is not implemented in TasTools, however, as its use can significantly reduce the enjoyability of the resulting TAS due to the screen shaking haphazardly, effectively transforming the resulting videos into some psychedelic art. Furthermore, the advantages of VC over the simple anglemod compensation described previously are largely negligible. It is for these reasons that we decided against implementing VC in TasTools, though the technique will still be described here for academic interests.

The idea is the following: while the yaw angle in degrees is always a multiple of $𝑢$ , we can adjust the values of cl_forwardspeed and cl_sidespeed in combination with cl_yawspeed so that the polar angle of $ˆ 𝐚$ can reside between any two multiples of $𝑢$ . As a result, the actual $𝜃$ can now be better approximated, hence higher strafing accuracy.

Have a look at the illustration below.

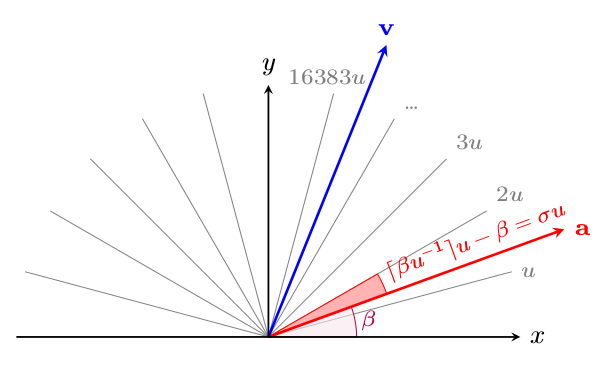
The $𝐚$ in the figure is the intended $𝐚$ . The actual $𝐚$ being computed by the game will likely be an approximation of the intended vector. Also, the spaces between the lines corresponding to the multiples of $𝑢$ are exaggerated so that they are easier to see. The figure above depicts strafing to the right.

The algorithm would begin with the decision to strafe left or right, then compute $𝜃$ in degrees, along with

𝛼 = a t a n 2 (𝑣 𝑦, 𝑣 𝑥) 𝛽 = 𝛼 \mp 𝜃 𝜎 = {⌈ 𝛽 𝑢 - 1 ⌉ 𝑢 - 𝛽 i f r i g h t s t r a f i n g 𝛽 - ⌊ 𝛽 𝑢 - 1 ⌋ 𝑢 i f l e f t s t r a f i n g

where the $\mp$ in $𝛽$ should be replaced by $-$ if right strafing and vice versa. The quantity $𝜎$ has the following meaning: $⌈ 𝛽 𝑢 - 1 ⌉ 𝑢 - 𝛽$ represents the difference between $𝛽$ and the smallest multiple of $𝑢$ not lower than $𝛽$ , while the other represents the difference between $𝛽$ and the largest multiple of $𝑢$ not greater than $𝛽$ . It is exactly these differences that we are compensating in this algorithm.

Now we must find $𝜙 = a r c t a n (𝑆 / 𝐹)$ with $𝐹 \geq 0$ and $𝑆 \geq 0$ so that $𝜙 - ⌊ 𝜙 𝑢 - 1 ⌋ 𝑢$ closely approximates $𝜎$ . A naive, inefficient and hackish way would be: for all $(𝐹, 𝑆)$ pairs with $‖ ⟨ 𝐹, 𝑆 ⟩ ‖ \geq 𝑀$ , compute the associated $𝜙 - ⌊ 𝜙 𝑢 - 1 ⌋ 𝑢$ and then find the one which approximates $𝜎$ to the desired accuracy. The problem with this approach, leaving aside its crudeness, is that there are about 4 million $(𝐹, 𝑆)$ pairs that satisfy the above constraint with $𝑀 = 320$ , which translates to 4 million arc tangent computations per frame. This takes about 0.25s on a modern 2.0 GHz Core i7.

TODO

Delicious recipes¶

We will provide some implementations of basic strafing functions in Python. import math is required.

The following function returns speed after one frame of optimal strafing.

def fme_spd_opt(spd, L, tauMA):
    tmp = L - tauMA
    if tmp < 0:
        return math.sqrt(spd * spd + L * L)
    if tmp < spd:
        return math.sqrt(spd * spd + tauMA * (L + tmp))
    return spd + tauMA

If computing the velocity vector is required, instead of just the speed, then one might use the following implementation, where d is the direction: 1 for right and -1 for left.

def fme_vel_opt(v, d, L, tauMA):
    tmp = L - tauMA
    spd = math.hypot(v[0], v[1])
    ax = 0
    ay = 0
    if tmp < 0:
        ax = L * v[1] * d / spd
        ay = -L * v[0] * d / spd
    elif tmp < spd:
        ct = tmp / spd
        st = d * math.sqrt(1 - ct * ct)
        ax = tauMA * (v[0] * ct + v[1] * st) / spd
        ay = tauMA * (-v[0] * st + v[1] * ct) / spd
    else:
        ax = tauMA * v[0] / spd
        ay = tauMA * v[1] / spd
    v[0] += ax
    v[1] += ay

On the other hand, if we want to compute the velocity as a result of an arbitrary $𝜃$ then we would instead use

def fme_vel_gen(v, theta, L, tauMA):
    spd = math.hypot(v[0], v[1])
    ct = math.cos(theta)
    mu = L - spd * ct
    if mu < 0:
        return
    if tauMA < mu:
        mu = tauMA
    st = math.sin(theta)
    ax = mu * (v[0] * ct + v[1] * st) / spd
    ay = mu * (-v[0] * st + v[1] * ct) / spd
    v[0] += ax
    v[1] += ay

Note that these two implementations will no work if the speed is zero. This is a feature and not a bug: when the speed is zero the direction is undefined. In other words, the meaning of “rightstrafe” or “leftstrafe” will be lost without specifying additional information.

For backpedalling, we have

def fme_spd_back(spd, L, tauMA):
    return abs(spd - min(tauMA, L + spd))

Then we have the following function which applies friction. This function must be called before calling the speed functions when groundstrafing.

def apply_fric(spd, E, ktau):
    if spd > E:
        return spd * (1 - ktau)
    tmp = E * ktau
    if spd > tmp:
        return spd - tmp
    return 0